Modellierung dynamischer Prozesse mit Differentialgleichungen (DGLs) und deren Parameterschätzung mit dem Excel® Solver

Einleitung

Dieses Projekt wird aktuell aufgebaut/erweitert. Schauen Sie in naher Zukunft wieder vorbei, aktueller Stand der Entwicklung: April 2022

Zusammenfassung: Dieses Projekt erarbeitet und beschreibt eine Möglichkeit, wie man in Excel® mit Hilfe des implementierten Solvers die Parameterschätzung von numerisch gelösten Differentialgleichungen, bzw. -systemen, erfolgreich durchführen kann.

In diesem Projekt wird nicht das Verhalten von Differentialgleichungen (DGLs) bei Änderungen der Parameter diskutiert, wir verwenden solche Modelle einfach als Regressionsfunktionen für die Analyse von Feld- und Laborversuchen verschiedenster Forschungsrichtungen. Oder einfach ausgedrückt, wir stellen ein möglichst simples Verfahren zur Parameterschätzung von Differentialgleichungen vor. Das bedeutet, es müssen zwei Probleme simultan berücksichtigt werden. Erstens die Identifizierung eines Modells, basierend auf Differentialgleichungen, welches die zugrundeliegenden Daten abbilden kann, und zweitens wie dieses Modell an die Daten angepasst werden kann. Da Differentialgleichung in den seltensten Fällen analytisch lösbar sind, sind demnach 2 numerische Prozesse notwendig, wiederum simultan. Zuerst erfolgt die numerische Integration der DGL über ein entsprechendes Verfahren, wie z.B. Euler, Runge-Kutta (RK) oder RK-Fehlberg (RKF). Im zweiten Schritt wird ein Parameterschätzverfahren angewandt, um den Vektor zu identifizieren, der die Daten am besten abbildet. Die Diskussion über die Problematik solcher kombinierter, numerischer Verfahren wird den Mathematikern überlassen und ist nicht der Schwerpunkt dieses Projekts. Beide Verfahren stehen potentiell in Excel zur Verfügung. Während der Solver ein Standard Add-In für Parameterschätzprobleme ist, stehen zahlreiche numerische Integratoren zum Download aus dem Internet zur Verfügung. Der Hintergrund, wie der Solver Optima anpasst, ist nicht bekannt, aber die bisherigen Erfahrungen haben gezeigt, dass der Anpassungsalgorithmus (visuell) lokale Optima vermeidet, er kann relativ komplexe Modellstrukturen und Kurven mit ausreichender Güte anpassen.

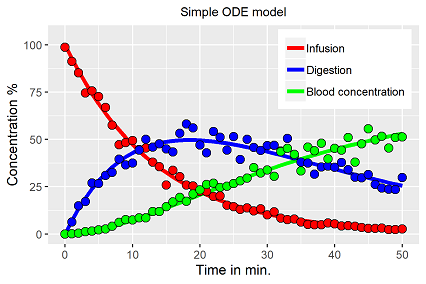
Die Herausforderung ist scheinbar sehr einfach, wie man die Aufgabe realisieren kann ist der Grund dieses Projekts. Solver maximiert (oder minimiert) den Wert einer Zielzelle durch Variieren der Werte eines Parametervektors. Soweit uns bekannt, ist Solver einmal gestartet, wird der gesamte Iterationsprozess durchgeführt, aber theoretisch müsste nach jeden Parameterwechsel der Solver gestoppt werden und der Integrator der numerischen Lösung muss gestartet werden. Eine (aber sicher nicht die einzige) Lösung für dieses Problem: eine VBA Funktion mit der Liste veränderlicher Variablen, die mit der Zielzelle verknüpft ist. Bei Änderung einer Variablen wird daraufhin automatisch der Integrator und löst das komplette Differentialgleichungssystem mit dem neuen Parameterwert. Um den Effekt der Parameteränderung zu quantifizieren, muss die gesamte Statistik (z.B. die quadrierten Residuensummen, o.ä.) komplett auf dem VBA Level berechnet werden.

Beispiel:

Nehmen wir an, Zelle Q8 des Arbeitsblattes ist die zu optimierende Zielzelle, in deren Wert alle notwendigen Berechnungen zusammengefasst sind. Die Zielzelle enthält folgende Funktion:
=InitiateRSSCalculation (Q3; Q4; Q5)
mit den drei zu schätzenden Variablen der DGL in Zelle Q3, Q4, Q5.

Auf dem VBA level ist die Zielzellenfunktion wie folgt programmiert:
Function InitiateRSSCalculation (para1 As Double, para2 As Double, para3 As Double)
RSSCalculation para1, para2, para3
InitiateRSSCalculation = para1
End Function
ruft die Hauptroutine RSSCalculation mit dem numerischen Integrator und der Residuenberechnung auf. Der Rückgabeparameter para1 wird zurück an Zielzelle Q8 übermittelt.

Für jede noch so marginale Änderung eines Parameterwertes durchläuft die Hauptroutine das Gesamtsystem der Differentialgleichungen.

Die Struktur des folgenden Hauptprogramms Sub RSSCalculation(par1 As Double, par2 As Double, par3 as Double) ist eher als eine To-Do Liste anzusehen.

Folgende Komponenten sind Bestandteil der Hauptroutine:

Initiierung und setzen der notwendigen Parameter
Transfer der Messwerte vom Arbeitsblatt zu einem entsprechenden VBA Array;
Definieren des Modells anhand des DGL-Systems;
Setzen der Anfangswerte (sehr wichtig!);
Durchlauf der numerischen Integrationsschleife für die gewählte x-Achse oder Zeitachse;
Vergleich des DGL Ergebnisses mit den Messwerten zu jedem Termin und Residuenberechnung zu jedem Zeitschritt;
Ende der Integrationsschleife;

Berechnung der resultierenden Residuensumme oder eines R² oder eines Maximum Likelihood Wertes, je nachdem man für den Vergleich gewählt hat. Der Wert wird an die aufrufende Funktion InitiateRSSCalculation zurückgegeben und verändert automatisch den Wert der Zielzelle Q8.

Man kann die Liste der Parameter bei der Funktionsübergabe nicht durch Bereichsdefinitionen vereinfachen, z.B. “Q3:Q5”. (Jemand kennt bestimmt eine elegantere Lösung, aber nicht ich), jeder Parameter muss auf allen Ebenen separat definiert werden;
R² - Werte sind bei nicht-linearen Modellen wenig aussagekräftig, aber es hilft ein relatives Gefühl für die Güte einer Anpassung zu erhalten. Da der Parameter dimensionslos ist, ist er auf alle Skalenebenen anwendbar;
Die Berechnung der Varianzen und Konfidenzbänder der geschätzten Parameter ist momentan nicht Ziel dieses Projekt, und verbleibt für den Endanwender;

Nachdem das Grundkonzept prinzipiell aufgestellt ist, kann man mit Hilfe des Solver alle Parameter simultan anpassen (Limitiert auch durch die restriktive Anzahl der erlaubten Parameter in Solver). Bei den Einstellungen in der Solver Add-in sind sowohl die Zielzelle Q8 als auch die Variablenzellen (Q3; Q4; Q5) entsprechend anzugeben. Wenn die Anpassungskriterien die RSS sind, wird die Zielzelle minimiert, wenn der R²-Wert Verwendung findet, wird die Zielzelle maximiert. Erhalten der Lösung durch den entsprechenden Auslöseschalter. Alternativ, und manchmal auch interessanter, kann man den VBA Code des Solver verwenden, indem man den Verweis für den Solver in VBA setzt. Es ist müßig zu erwähnen, aber das Solver Add-in muss in VBA natürlich installiert sein.

Je nach Modellkomplexität, zu schätzenden Parameteranzahlen und Computergeschwindigkeit dauert die doch sehr umständliche Berechnung eine Weile.

Das System ist beliebig in jede Richtung erweiterbar , erlaubt sowohl die Lösung komplexer horizontaler Modelle, als auch vertikale Regressionsmodelle, z.B. zur Identifizierung und Quantifizierung entsprechender Responsefunktionen. Es obliegt dem Anwender wie komplex sein Modell sein soll und ob er es auch noch beherrscht, ohne den Überblick zu verlieren. Die ganze Herausforderung besteht darin die Gesamtkomplexität auf einen Zellwert zu kondensieren. Und nochmals, die Grenzen sind auch durch die Parameterkapazität des Solver gesetzt (jedenfalls in den Excel Versionen). Auch ohne die Verwendung des Solver wird die Modellentwicklung durch das System hinsichtlich der Plausibilität extrem vereinfacht. Die direkte Überprüfung des Modellverhaltens bei Parameteränderungen erlaubt eine schnelle Orientierung über a) den möglichen Parameterraum und b) ob das Modellverhalten die durch Messwerte charakterisierte Situation/Realität überhaupt abbilden kann, d.h. sind die Modellannahmen korrekt?

Empfehlung: DGLs verhalten sich manchmal in gewissen Parameterbereichen "fürchterlich" (chaotisch), und Nemaplot ist sich bewusst, der Anwender hat eine ausreichende Anzahl von Funktionen zur Verfügung, um solche numerische Integratoren wie den hier vorgestellten RKF in die Knie zu zwingen. Das ist sicherlich keine Schwierigkeit. Ein weiteres Problem sind plötzliche Wechsel auf der x-Achse, auch dann kommen die Integratoren schnell an ihre Grenze und sollten unbedingt vermieden werden. Das heißt, sogenannte 0,1 Funktionen sind vom Prinzip her nicht erlaubt. Zu umgehen ist es Beispiel: sogenannte Schaltfunktionen, welche dynamische Prozesse starten oder stoppen, müssen folgende Bedingungen erfüllen: a) sie müssen für jeden Integrationsschritt definiert sein und b) potentielle numerische Overflows müssen vermeidbar sein (selbst bei heutigen Rechnern). Da diese Schaltfunktionen über den gesamten Integrationszeitraum mitgeschleppt werden, können zu Beginn und Ende der Integration extrem hohe/niedrige Werte auftreten, die das Programm zum Absturz bringen.