Modellierung dynamischer Prozesse mit Differentialgleichungen (DGL) und deren Parameterschätzung mit dem Excel® Solver
Beispiel des Wachstums von Melonen als Funktion der Temperatur
Zusammenfassung: Am Beispiel der vorhandenen Daten zum Wachstum von Melonen bei verschiedenen konstanten Temperaturen wird ein entsprechendes Differentialgleichungsmodell für das Experiment mit mehreren Faktorstufen aufgestellt, (das Wachstum wurde bei konstanten Temperaturen im Bereich von 20°C bis 37.5°C durchgeführt) und die Parameterschätzung in Excel® mit Hilfe des implementierten Solver durchgeführt. Die bestehenden Ansätze der horizontalen Regression (über die Zeit) werden um die vertikalen Regressionskomponenten (Faktorstufen, Temperaturstufen, etc.) erweitert. Der Schwerpunkt liegt in der Gegenüberstellung der zweistufigen Verfahren versus der simultanen Anpassung über alle Experimente.
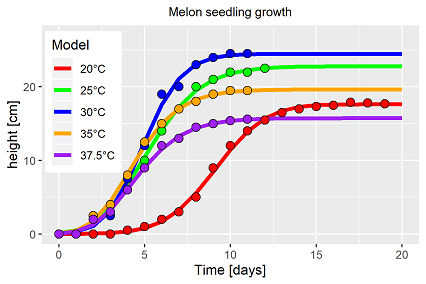
Das Wachstumsmodell basiert auf den Daten der Wachstumshöhe von Melonensetzlingen bei verschiedenen konstanten Temperaturen (Pearl et al., 1934, Daten entnommen aus "Models in Biology", 1994)1. Während Brown & Rothery (1994)1 sich ausschließlich auf den Nachweis über die Möglichkeit der Modellanpassung der Richardsfunktion beschränken, bieten die Daten aufgrund ihrer Komplexität wesentlich interessantere Herausforderungen. In der Kurzbeschreibung ergeben sich folgende Bezugsgrößen: sowohl die Wachstumsraten als auch die Wachstumshöhe sind abhängig von der Temperatur, also nichts Ungewöhnliches. Besonders macht diesen Datensatz die Verwendung sehr hoher Temperaturen bis in den supraoptimalen Bereich hinein (Abb. 1).
Zur Modellierung der Wachstumsdynamik wird ein einfaches exponentielles DGL-Modell mit einer entsprechenden Abschaltfunktion eingeführt (Gl. 1) Die Pflanzen wachsen mit der Rate r bis die Zeit t den kritischen Zeitwert tc erreicht.
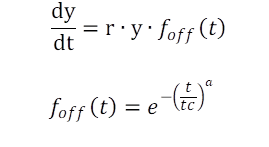
Fall 1: Parameterschätzung im Zweistufenverfahren
Im ersten Schritt wird Gl. 1 an die Daten jeder Temperaturstufe angepasst. Abb. 1 stellt das Ergebnis graphisch da. Gl. 1 ist für allgemein anwendbar und führt zu einem individuellen Parametervektor für jede Temperaturstufe (Tab. 1). Im Gegensatz zu den Aussagen von Brown & Rothery (1994)1 können die Daten in einem gemeinsamen Grundmodell mit ausreichender Präzision (R2>0.99) dargestellt werden (Abb. 1).
| Tab. 1: resultierende Parameterwerte für das DGL Modell | |||||
|---|---|---|---|---|---|
| Parameter | 20°C | 25°C; | 30°C | 35°C | 37,5°C |
| r | 0.81 | 1.48 | 1.59 | 1.70 | 1.55 |
| tc | 8.28 | 4.63 | 4.39 | 3.95 | 4.15 |
In 2. Schritt werden die Parameter r (für Wachstum) und 1/tc (für Entwicklung) durch eine entsprechende Temperaturresponsefunktion anpasst. (Wir verwenden im Allgemeinen die O'Neill-Funktion, aufgrund der Komplexität und der zahlreichen Wiederholungen wird auf entsprechende Artikel, Seite 2 verwiesen). Mit vier zu schätzenden Parametern (rmax, Q10, Topt & Tmax) bei 5 "Messwerten" (= primäre Parameter aus der ersten Anpassung) sind die Basisbedingungen gerade so gegeben.
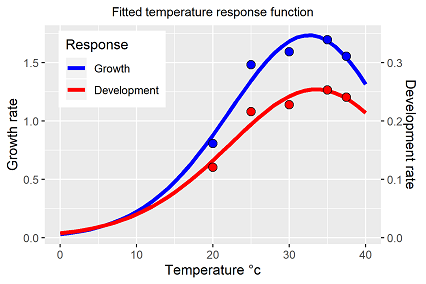
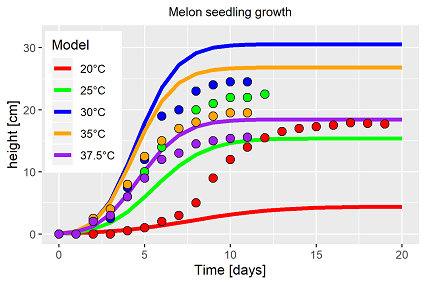
Abb. 2 stellt die Anpassung an die Temperaturfunktion graphisch dar, die Funktion ist gut geeignet die Temperatureinflüsse funktional abzubilden.
Auf die unterschiedlichen Skalierungen der beiden y-Achsen in Abb. 2 wird hingewiesen. In der Ergebnisvalidierung werden die geschätzten Parameter der Temperaturresponsefunktionen
wieder in das Ursprungsmodell eingesetzt. Theoretisch müsste sich ein gemeinsamer Parametervektor für alle Temperaturstufen ergeben. Das Ergebnis in Abb. 3 verdeutlicht mehr
als deutlich das Scheitern dieser Vorgehensweise.
Im Folgenden wird daher ein alternativer Lösungsweg vorgestellt.
Fall 2: Simultane Parameterschätzung über alle Temperaturstufen
Zur Einleitung der simultanen Parameterschätzung müssen zwei weitere Grundlagen vorgestellt werden. Gl 2. stellt das zu lösende Minimierungsproblem vor: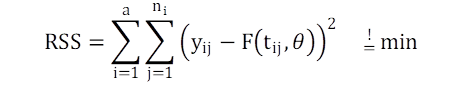
mit a = 5 Temperaturstufen, und ni die Anzahl der Messung der Temperaturstufe i. Anhand der Messwerte j der Temperaturstufe i werden in Bezug auf die
Funktionswerte zum Zeitpunkt ti,i bei gegebenen Parametervektor θ die Residuensummen minimiert.
Das Grundmodell wird bezüglich der Simultananpassung wie folgt erweitert (Gl. 3):
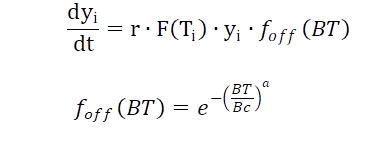
wobei die Wachstumsrate r mal F(T)i natürlich die obige O'Neill-Funktion über die Temperatur i ist. Der Abschaltzeitpunkt wird ebenfalls über die Temperatur als sogenannte Biologische Zeit definiert, d.h. es werden die Summen der 1/Entwicklungszeiten für jede Temperatur gebildet, ebenfalls auf der Basis der gegebenen Temperaturresponsefunktion. Das Wachstum stoppt, wenn eine kritische biologische Zeit Bc überschritten ist.
Um im Sinne die Modelle möglichst einfach zu halten, wurde die Simultanschätzung zuerst mit einer gemeinsamen Temperaturfunktion für beide Faktoren, Wachstum und Entwicklung, durchgeführt. Abb. 4 verdeutlicht das Ergebnis. Der Solver approximierte immer wieder zu diesem "Optimum", was zu dem Rückschluss führt, dass die Modellannahmen unzureichend sind.
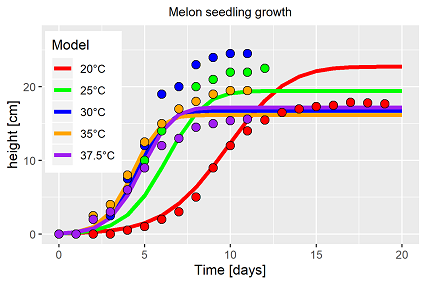
Das unzureichende Ergebnis ist nicht überraschend, da die Einzelanpassungen schon angedeutet haben, dass Wachstum und Entwicklung unterschiedlich auf den Faktor Temperatur reagieren (Abb. 2). Es musste aber die Hypothese getestet werden, ob über den Solver ein zufriedenstellendes mittleres Modell geschätzt werden könnte. Dies war nicht der Fall. Das Modell wurde daher um je eine der verwendeten Temperaturfunktionen für beide Größen, Wachstum (g ~für growth) und Entwicklung (d ~ für development), erweitert. Die Ergebnisse sind in Abb. 5 und 6 dargestellt.
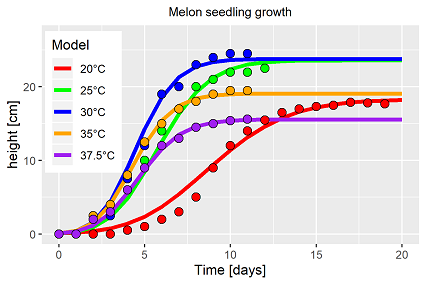
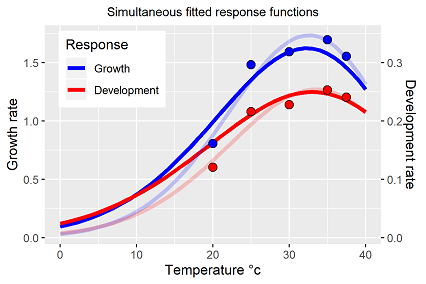
Tatsächlich findet der Solver eine Lösung für das erweiterte Modell, welches alle Daten über die fünf Temperaturstufen zur Schätzung verwendet und mit sehr guter Güte abbildet (Abb. 5). Die Temperatur wirkt sich in zweifacher Hinsicht in unterschiedlicher Intensität auf das Pflanzenwachstum (der Melonen) aus, so dass für jeden der Prozesse (Wachstum, Entwicklung) eine eigene Temperaturresponsefunktion nötig ist. Transferiert man die aus dem Gesamtmodell geschätzten Parameter der resultierenden Temperaturresponsefunktionen auf die Ergebnisse aus den Einzelanpassungen (schattierte Linien) zeigen sich geringe Abweichungen (Abb. 6). Im statistischen Sinne wahrscheinlich noch nicht mal verschieden, sind die Unterschiede aufgrund der verschachtelten Nichtlinearitäten von Wachstumsmodell und eingebetteten Temperaturresponsefunktionen mehr als bedeutend. In Tabelle 2 ist der sich ergebende Parametervektor des Gesamtmodells (Gl. 3) aus mehreren Gründen noch mal zusammengefasst:
| Tabelle 2: resultierende Parameterwerte für das DGL Modell mit 2 Temperaturfunktionen | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | y0 | rg | Q10g | Toptg | Tmaxg | rd | Q10d | Toptd | Tmaxd | Bc | α |
| Schätzer | 0.1 | 1.625 | 1.949 | 32.284 | 89.335 | 1.054 | 1.832 | 33.018 | 100.0 | 4.536 | 2.003 |
- Die Anfangswerte y0,iwurden für alle Temperaturstufen gesetzt.
- Die Schätzer in Tabelle 2 repräsentieren einen extrem engen Parameterkorridor (~vielleicht sogar die "perfekte" Lösung?), schon kleinere Abweichungen in den Schätzwerten führen zu überproportionalen Abweichungen in den Trajektorien. Dies weist natürlich auf eine gewisse Instabilität hin, aber, der Datensatz definiert die Grenze, nicht die zugrundeliegende Mathematik.
- Der Solver approximiert nicht bei den Tmax-Werten. Die vorgegebenen, sehr hohen Grenzwerte wurden erreicht. Aber wählt man kleinere Grenzwerte, approximiert das ganze Modell nicht, d.h. auch wenn die Schätzwerte von Tmax komplett unrealistisch sind, sie haben ihre Berechtigung.
- Die simultane Anpassung von nichtlinearen Systemen ist im Ergebnis und Aussagekraft dem Zweistufenverfahren eindeutig überlegen, vor allem wenn man übertragbare Gesetzmäßigkeiten erkennen und analysieren will.
- Die Verwendung des Solver ermöglicht Genauigkeiten in den Parametern, die weit aussagekräftiger sind als sogenannte Anpassungen per Hand.
- Die Frage nach dem Temperaturoptimum ("25°C bis 35°C", Brown & Rothery (1994), eine Erkenntnis auch ohne jegliche Modellierung!) kann jetzt wesentlich genauer quantifiziert werden.
Resümee
Ein einfacher Datensatz, uralt, vielleicht sogar trivial, extrem herausfordernd. Wir hinterfragen nicht ob die Ursprungsautoren Pearl et al., 1934) wirklich in der Lage waren, konstante Temperaturen über die Versuchsdauer aufrechtzuerhalten. Selbst heutzutage ist das ein schwieriges Unterfangen. Das ist aber nicht von Belang. Das Ergebnis beinhaltet das reale, aber letztendlich unbekannte Temperaturszenario der Versuche von 1934. Zu Beginn dieser Modellübung war es nicht klar, ob es überhaupt zu einem Ergebnis kommen wird, das in dieses Projekt über die Parameterschätzung von Differentialgleichungen aufgenommen werden kann. Das Ergebnis war völlig offen, die Aussagen von Brown & Rothery (1994) wurden nicht angezweifelt. Diese Daten und die hier vorgestellte Analyse ermöglichen für die klassische Frage der Bestandesdynamik, wie viel ist Wachstum, wie viel ist Entwicklung, eine Lösung anzubieten. Ohne jetzt ins Detail der Interpretation dieser Ergebnisse zu gehen, die hier vorgestellten Verfahren demonstrieren die Möglichkeiten, wie die iterativen Prozesse von Arbeitshypothesen erstellen, damit Modellannahmen zu verknüpfen und mit Hilfe des Solver (oder den ähnlichen Verfahren in Matlab, Phyton, etc.) eine Lösung zu erhalten, bis plausible Ergebnisse erreicht sind (wenn es sie dann gibt). Eine Anmerkung zum Abschluss: Die Literatur ist bei temperatursensiblen Prozessen (z.B. Verderbskinetik, Bestimmung der Haltbarkeitsdauer, Bakterienwachstum) voll von Temperaturresponsefunktionen, z.B. die Arrheniusgleichung, wobei immer wieder die allgemeine Übertragbarkeit der geschätzten Funktionsparameter im Vordergrund steht. Aber, was eben auch hier der Fall ist, die Verschachtelung mehrerer nichtlinearer Zusammenhänge von Modell und Responsfunktion führt zu einem untrennbaren Ganzen. Die Wahl des Wachstumsmodell beeinflusst daher auch die Parameter der Temperaturresponsefunktion, will man eine Übertragbarkeit erreichen, müssen beide, bzw. bei größeren Systemen, alle Komponenten als eine Einheit berücksichtigt werden.
Literatur:
1Models in Biology, Mathematics, Statistics and Computing, D. Brown & P. Rothery, (1994), Seite 50.
 Evaluation reinvented
Evaluation reinvented
